

I can even add another infinite aleph-null of lines and still not change the quantity. I can even add two more lines, three more, four more-I always end up with only aleph-null things. Clearly the amount of lines hasn’t changed. I just start here and then continue from the beginning. There are still only aleph-null lines here because I can match the naturals one-to-one just like before. Unending amounts aren’t like finite amounts.
#Infinity times 0 plus
Both sets have the cardinality aleph-null.īut what happens when I do this? Now how many lines are there? Aleph-null plus one? No. There’s always a next natural, but there’s also always a next line. The number of lines here is equal to the number of natural numbers that there are. If we draw a bunch of lines and make each next line a fraction of the size and a fraction of the distance from each last line, well we can fit an unending number of lines into a finite space. How? Well, let’s use our old friend, the super-task. A googol, a googolplex, a googolplex factorial to the power of a googolplex to a googolplex squared times Graham’s number? Aleph-null is bigger. The point is, aleph-null is a big amount bigger than any finite amount. That may sound surprising, since fractions appear more numerous on the number line, but as Cantor showed, there’s a way to arrange every single possible rational such that the naturals can be put into a one-to-one correspondence with them. It’s also how many even numbers there are, how many odd numbers there are it’s also how many rational numbers-that is, fractions-there are. Aleph is the first letter of the Hebrew alphabet, and aleph-null is the first smallest infinity. Instead, there is a unique name for this amount: ‘aleph-null’ (ℵ 0). We use the natural numbers-that is, 0, 1, 2, 3, 4, 5 and so on-as cardinals whenever we talk about how many things there are, but how many natural numbers are there? It can’t be some number in the naturals, because there’ll always be 1 plus that number after it. We can demonstrate this equality by pairing each member of one set one-to-one with each member of the other. Now, two sets have the same cardinality when they contain the same number of things. 20 is the ‘cardinality’ of this set of dots. When a number refers to how many things there are, it is called a ‘cardinal number’. Let’s visit some of them and count past them.įirst things first. You need infinite numbers to talk about and compare amounts that are unending, but some unending amounts-some infinities-are literally bigger than others. So there is no biggest, last number… except infinity? No. Oh and then there’s 42, and 43 … a billion, a trillion you know, no matter how big of a number you can think of, you could always go higher. 40 is the biggest number … on Earth in terms of surface area.īut in terms of amount of things, which is normally what we mean by a number being ‘big’, 40 probably isn’t the biggest. On the other hand, it is not possible to prove anything about the limit of f(x)*g(x) without more information about the functions.What is the biggest number you can think of? A googol? A googolplex? A milli-million-oplex? Well in reality, the biggest number is 40.Ĭovering more than 12,000 square metres of Earth, this 40, made out of strategically-planted trees in Russia, is larger than the battalion markers on Signal Hill in Calgary, the 6 found on the Fovant Badges in England-even the mile of pi Brady unrolled on Numberphile. It is easy to prove that f(x)/g(x) tends to infinity as x tends to infinity. Suppose f(x) tends to infinity and g(x) tends to zero as x tends to infinity. Since the result could be anything from very small through very big, NaN is the most reasonable answer.Īlthough I think the above is the best way to understand practical floating point behavior, a similar issue arises in real number limits. Something very big multiplied by something very small could be anything, depending on the actual magnitudes that we don't know. Something very big divided by something very small is very, very big, so `Infinity / 0 = Infinity". NaN represents either "No real number result", for example sqrt(-1), or "Haven't a clue". Similarly, each infinity also represents all numbers with the corresponding sign that would round to something with a magnitude that would not fit in the finite range. Even tiny numbers do have a sign if they are not actually zero. They also represent all real numbers that would round to something smaller than the smallest subnormal.
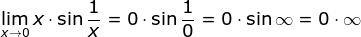
The floating point zeros not only represent the real number zero. It is easier to understand the behavior of IEEE 754 floating point zeros and infinities if you do not think of them as being literally zero or infinite.


 0 kommentar(er)
0 kommentar(er)
